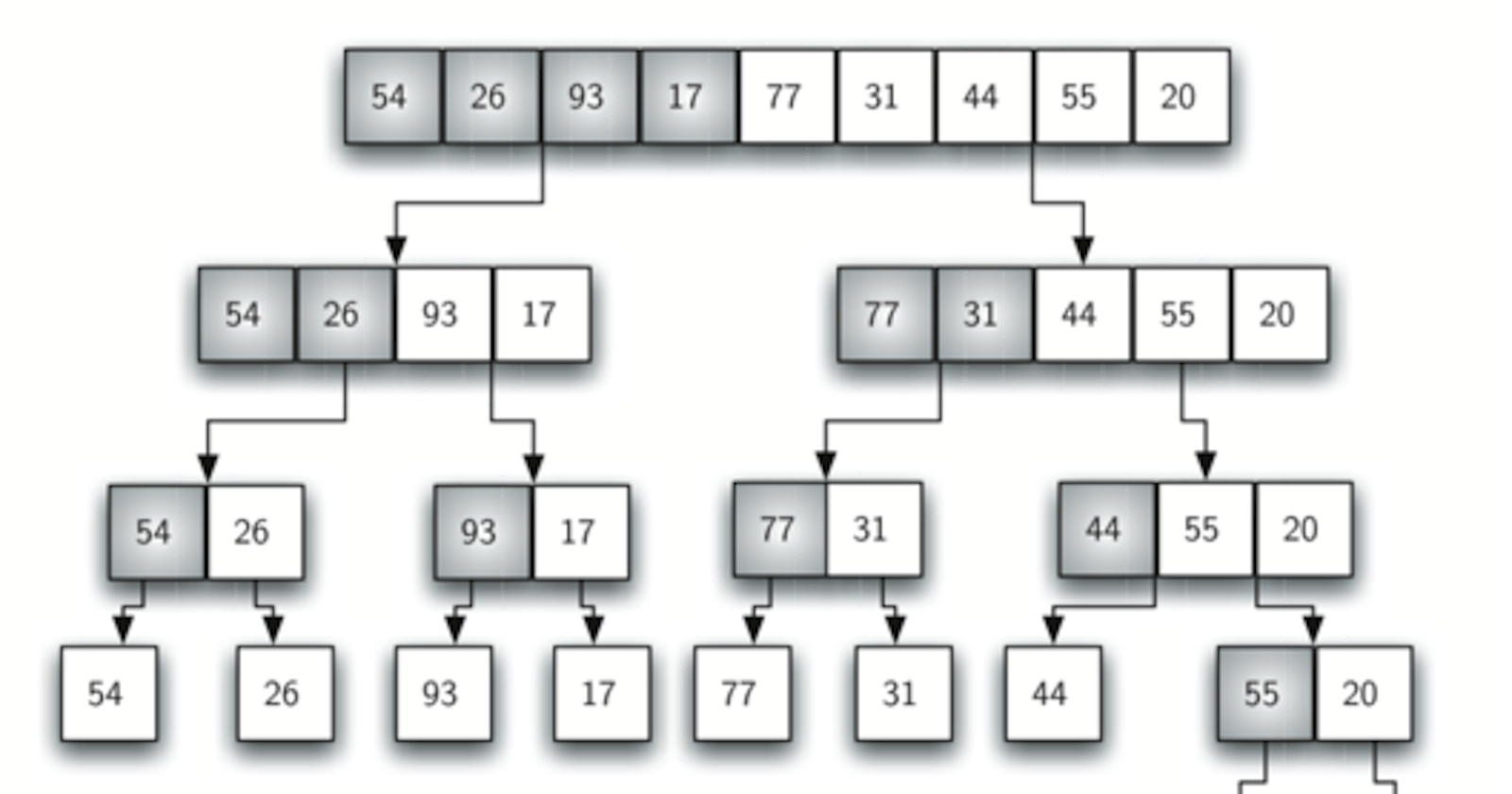
MergeSort splits an array into halves which takes log(n) time and then takes n operations to sort the entire list when we are merging it back after breaking the halves down. Therefore, it has a complexity of O(n log(n))

How it works:

Take array, arr = [54, 26, 93, 17, 77, 31, 44, 55, 20] size, n = 9

MergeSort will take this array and recursively break it into halves (leftHalf, rightHalf in code) till it reaches a single element of size 1 which of its own is already sorted.

Now using the size 1 leftHalf and righHalf array (which are already sorted) it will combine these two arrays and combine them into sorted manner.

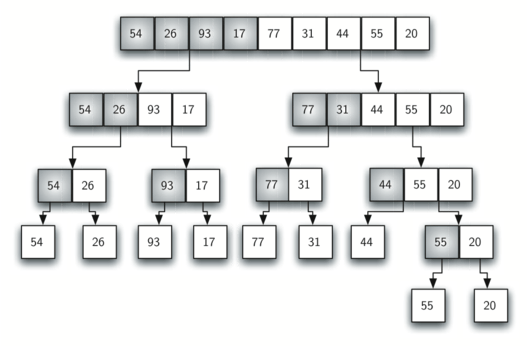
Now we could sort array where size of leftHalf & rightHalf > 1 and leftHalf and rightHalf in of itself will be sorted since after breaking them down recursively we are combining them back in a sorted manner.

def mergeSort(arr):
    # if arr size is < 1 just return arr else do mergeSort computation
    if len(arr) > 1:
        mid = len(arr)//2

        # break the arr down into left and right until it becomes a size of 1
        leftHalf = mergeSort(arr[:mid])
        rightHalf = mergeSort(arr[mid:])

        # used to iterate leftHalf, rightHalf, and 
        # arr (we will overwrite the array given to us using this k)
        i, j, k = 0, 0, 0

        # we will iterate through the leftHalf and rightHalf of the array
        while i < len(leftHalf) and j < len(rightHalf):
            if leftHalf[i] < rightHalf[j]:
                # overwrite the original arr (we don't need to worry about losing any values
                # since leftHalf would have it already stored)
                arr[k] = leftHalf[i]
                #increment i by 1 since we have now used i element of leftHalf
                i += 1
            else:
                arr[k] = rightHalf[j]
                j += 1
            # increment k since added leftHalf or rightHalf smallest array
            k += 1

        #it could be the above while condition ended early 
        # j could have reached the end of rightHalf since it had more
        # smaller values and leftHalf still has values within it that haven't been used
        while i < len(leftHalf):
            arr[k] = leftHalf[i]
            i += 1
            k += 1

        while j < len(rightHalf):
            arr[k] = rightHalf[j]
            j += 1
            k += 1

    return arr

print(mergeSort([54, 26, 93, 17, 77, 31, 44, 55, 20]))